Sebesség
Az ejtőernyő működésbe hozásának pillanatától kezdve egészen addig, amíg az ejtőernyős földet nem ér, mozgásban van. Ezért az ejtőernyős ugrás elméletének vizsgálatakor mindenekelőtt a sebesség fogalmát kell tisztázni, mely a mozgás fő jellemzője.
A sebesség a test időegység alatt megtett útja, jele V. A sebességet egy másodperc alatt megtett méterekben (m/mp) vagy egy óra alatt megtett kilométerekben (km/ó) mérik.
Ha a sebesség m/mp-ben van megadva és ezt km/ó-ra kell átszámítani, akkor az m/mp értéket meg kell szorozni 3,6-tal. Például 10 m/mp sebesség 36 km/ó sebességgel egyenlő (10×3,6 = 36).
Ha viszont a km/ó-ban kifejezett sebességet kell m/mp-re átszámítani, akkor a km/ó-ban megadott sebességet 3,6-tal kell elosztani. Például 180 km/ó egyenlő 50 m/mp-cel (180:3,6 = 50).
Ha a test egyenletes sebességgel mozog, a sebesség a következő képlet alapján határozható meg:
v = s / t
ahol s = megtett út
t = mozgás ideje.
Ha a mozgási sebesség a vizsgált úton nem állandó, akkor az egész utat el kell osztani a mozgási idővel s így megkapjuk az átlagos sebességet, vagyis
vátl = s / t
Minél kevésbé változik a sebesség a mozgási idő alatt, annál közelebb van az átlagos sebesség az egyes útszakaszok tényleges sebességéhez. Az átlagos sebesség számunkra azért fontos, mert az ejtőernyős sportnál a gyakorlatban éppen az átlagos sebességet kell figyelembe venni. Így például a repülőgép átlagos sebességét, az ejtőernyő átlagos süllyedési sebességét stb. Ha feltételezzük, hogy az ejtőernyős H magasságban ugrott ki a gépből és T mp alatt ért földet, az átlagos süllyedési sebességet úgy számítjuk ki, hogy az utat elosztjuk az idővel, vagyis
Vátl = H / T
A nyitott ejtőernyővel való átlagos süllyedési sebességet a következőképpen határozzuk meg. Jelöljük a késleltetés idejét t-vel, a zuhanva megtett utat pedig h-val
Vátl = (H – h) / (T – t)
ahol (H-h) az az út, amelyet az ejtőernyős ejtőernyőjével (T-t) ido alatt megtett.
Gyorsulás
Legtöbbször olyan mozgás fordul elő, amelynek a sebessége változó. Ha ezt a mozgást vizsgáljuk, nemcsak azt kell tudnunk, hogy valamely időpontban mekkora a sebesség, hanem ezenkívül a sebességváltozást is ismernünk kell. Ezt a sebességváltozást gyorsulásnak nevezik. A gyorsulás az időegység másodperc alatti sebesség változása. Minthogy a sebességet másodpercekben méterenként fejezzük ki, a gyorsulást a másodpercre eső másodperc-méterben (m/mp2) fejezzük ki. A gyorsulást a-val jelölik.
Ha a mozgási sebesség nő, a gyorsulás pozitív, ha pedig csökken, akkor negatív.
A fentiek alapján a mozgás a sebességtől függően egyenletes vagy szabálytalan lehet. Az egyenletes mozgás lehet egyenletesen gyorsuló, ha a sebesség egyenletesen nő vagy egyenletesen lassuló, ha a sebesség egyenletesen csökken.
Az adott mozgás átlagos gyorsulását úgy kell kiszámítani, hogy az összes sebességváltozást el kell osztani azzal az idővel, amely alatt a sebességváltozás végbement.
Tegyük fel például, hogy a sebesség a mozgás kezdetén V1 és t idő múlva V2 lett. A gyorsulás az alábbi képlet alapján határozható meg.
a = (V1 – V2) / t
Ha tudjuk, hogy az ejtőernyőnek a kinyitástól a kinyílásig mekkora volt a sebessége, és ha ismerjük a kinyílási időt, akkor a képlet alapján meghatározhatjuk az ejtőernyő-rendszer kinyílási idő alatti gyorsulását.
Mozgási pálya
Azt a vonalat, amelyet a test mozgáskor lerajzol, mozgáspályának nevezzük. A mozgáspálya alakjától függően a mozgás lehet egyenesvonalú vagy görbevonalú (ha a mozgáspálya kör, parabola stb.).
Egyenesvonalú mozgást végez például a kezdősebesség nélkül ledobott test, a henger dugattyú stb. Görbevonalú mozgást végez például a bukfencező repülőgép, az ejtőernyős, aki vízszintesen repülőgépből ugrik ki stb. A körmozgás a görbevonalú mozgás gyakori esete.
A mechanika alaptörvényei
A mechanikának három alaptörvénye van.
Első törvény: Mindaddig, amíg valamely testre külső erő nem hat, annak sebessége – nagyságát és irányát tekintve – állandó. Tehát, ha valamely test nyugalmi helyzetben van, vagy egyenesvonalú egyenletes mozgást végez, az mindaddig nyugalmi helyzetben marad, illetve folytatja egyenesvonalú, egyenletes mozgását, míg valamely külső erő nem hat rá.
Ez a törvény a testnek azt a tulajdonságát fejezi ki, hogy ha külső behatás nem éri, megtartja sebességét. Az anyagnak ezt a tulajdonságát tehetetlenségnek, magát a törvényt pedig tehetetlenségi törvénynek nevezzük.
Második törvény: Minden – a testre ható külső erő – megváltoztatja, vagyis az erő irányában az erővel arányosan gyorsítja a test sebességét.
A második törvény a következő képlettel fejezhető ki:
P = m * a
ahol
P = erő kg-ban,
a = a test gyorsulás a m/mp2-ben,
m = a test tömege kg-ban.
A fenti képletből következik, hogy minél nagyobb valamely test tömege, annál nagyobb erőre van szükség azonos gyorsulás eléréséhez (a = P / m).
Nyilvánvaló, hogy minél nagyobb valamely test tömege, annál nagyobb ellenállást fejt ki a gyorsító, vagyis azon erőkkel szemben, amelyek sebességének mérvét vagy irányát meg akarják változtatni. Ezért a tömeget a test tehetetlenségi mérvének nevezik.
A fent elmondottakból következik, hogy két erő akkor egyenlő egymással, ha ugyanazon test mozgását – a gyorsulás nagyságát és irányát tekintve – ugyanolyan mértékben változtatja meg.
Ha megmérjük azt a gyorsulást, amely adott erő hatására keletkezik, meghatározhatjuk a test tömegét. A nehézségi erő (adott földfelületen) minden testnek egyenlő gyorsulást ad. Ennek a gyorsulásnak a jele g.
A nehézségi erőt a test súlyának nevezik. Ha az azonos helyen lemért testek súlyát összehasonlítjuk, ugyanakkor azok tömegét is összehasonlítjuk.
Harmadik törvény: Ha valamely testre erő hat, akkor feltétlenül vele egyenlő nagyságú, de ellenkező irányú erő is fellép. Ebből következik, hogy a természetben nincs egyedülálló erő, hanem az erő mindig páros. Ha például az asztalon fekvő ejtőernyő az asztalt nyomja, akkor az asztal ugyanolyan nagyságú, de ellentétes irányú erővel nyomja az ejtőernyőt. Röviden ez a mechanikai törvény a következőképpen hangzik: a hatás egyenlő a vele együtt ható ellenhatással.
A munka
A munka az erő és a megtett út szorzata, tehát munka = erő * út jelölése: W. A munka egysége a mechanikában a méterkilogramm, amely egy kilogramm erőnek egy méter úttal való szorzata.
1 kg súlynak 1 m magasságra való felemelése 1 mkg.
A mechanikában a munkán kívül használatos még egy sokkal általánosabb kifejezés, az energia, amely a munkavégzési képességet fejezi ki. Minthogy a természetben valamennyi erő munkát képes végezni, az energia fogalmát a természet minden jelenségénél alkalmazzák és ez valamennyi jelenség egységes mértéke.
A mechanikában kétféle energiát különböztetünk meg; mégpedig a kinetikai vagy mozgási energiát és a helyzeti energiát.
A kinetikai energia – a mozgás bármely pillanatában – egyenlő a test tömegének és a sebesség négyzetének a szorzata osztva kettővel, azaz
Ekin = (m * V2) / 2
A képletet más szóval elevenerőnek nevezik.
Tegyük fel például, hogy az ejtőernyős az ejtőernyő kinyílásának kezdetén V0 sebességgel, végén pedig Vn sebességgel halad. Az elevenerő-veszteség az ejtőernyő kinyílási ideje alatt tehát
E = (m * V02) / 2 – (m * Vn2) / 2
Ez a különbség az ejtőernyő kinyílási ideje alatt végzett W munkával egyenlő.
A levegő ellenállása
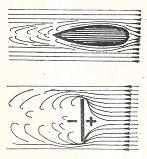
A levegőnek meghatározott tömege, nyomása és sűrűsége van. Ezért a levegőközegben mozgó test a levegő ellenállásának van kitéve. Minél sűrűbb az a légköri közeg, amelyben a test mozog, annál nagyobb lesz az ellenállása.
A levegő ellenállása függ a test alakjától és felületétől. Az érdes test felülete a leáramló levegő nagyobb súrlódását idézi elő, és ezáltal nagyobb a légellenállás, mint sima test esetén.
A test mozgásakor, annak felületéről leváló légörvényeket hoz létre, melyek a levegő ellenállásának fő okát képezik. Jól áramvonalazott sima felületű test esetén örvényleválás csak a test mögött keletkezik, a rosszul áramvonalazott szögletes testeknél viszont a teljes felületen.
Erős örvénylést előidéző testekre mindig nagy légellenállás hat. A légellenállás erejének meghatározásakor a test alakját egy bizonyos tényezővel vesszük figyelembe, amit szélcsatornában való kikísérletezéssel kapunk meg.
A testek jobb áramvonalazása esetén az ellenállási tényező kisebb, így pl. jól áramvonalazott test (cseppalak) esetén az ellenállás tényező 0,05; lemezesetén 1,28; ejtőernyő esetén 0,07-0,09.
Az ábrán azt látjuk, hogy egy négyszögletes lemez levegővel való leáramlásakor nagyobb örvénylés keletkezik, mint egy csepp alakú test leáramlásakor. A test méreteinek növekedésével arányosan nő a légellenállás, ami főképpen a test keresztmetszet területétől (főmetszettől) függ.
A levegő ellenállása a mozgási sebesség függvényében növekszik. A sebesség kétszeres növekedésekor a légellenállás négyszeresére nő: a sebesség háromszoros értékre való növekedésekor a légellenállás kilencszeresére nő. Ily módon a légellenállás a sebesség négyzetével arányos.
A levegőnek a test mozgásával szembeni ellenállását homlokellenállásnak nevezzük és ennek nagysága a következő képlet szerint számítható ki:

Q = 0,5 * C * p * V2 * S
ahol:
Q = az ellenállási erő kg-ban kifejezve,
C = ellenállás-tényező,
p = a mozgás sebessége m/mp-ben,
V = a test keresztmetszetének maximális területe,
S = m2-ben.
Az ejtőernyő – kupolával szemben támasztott követelmények
Az ejtőernyős süllyedési sebessége egyenes arányban van a levegő ellenállási erejével. Minél nagyobb az ellenállási erő, annál kisebb lesz az ejtőernyős süllyedési sebessége. Ily módon az ejtőernyők készítésekor rendszerint olyan alakot és kupolaterületet terveznek, hogy maximális legyen a levegőnek a süllyedő ejtőernyőkkel szembeni ellenállása. Azonban az ejtőernyő-kupola méreteinek túlzott növelése nem célszerű, mert ezáltal megnő az ejtőernyő súlya. Ezért törekednek, hogy minimális anyagfelhasználás mellett olyan kupolaalakot készítsenek, melynek maximális az ellenállása.
A nagy ellenállás fontos, azonban nem az egyetlen követelmény, amelyet az ejtőernyővel szemben támasztunk. A kupola alakja biztosítsa a gyors és megbízható nyitást és a stabil lengésmentes leereszkedést. Ezenkívül a kupolának erősnek, a készítésének és üzemeltetésének egyszerűnek kell lenni. Ezen követelmények általában egymással ellentmondóak. Például a nagy ellenállású kupola igen instabil, viszont megfordítva, az igen stabil kupola kis ellenállású. A szerkesztésnél ezeket az ellentmondásokat az ejtőernyők rendeltetésétől függően (mentőernyő, sportgyakorló ejtőernyő vagy teherernyő) oldják meg.
Az ejtőernyős mozgása a levegőben szabadeséskor
Légüres térben, ahol a test csupán a Föld vonzóerejének hatása alatt áll, az esési sebesség az esési idővel arányosan növekszik. Ebben az esetben a szabadon eső test sebessége az alábbi képlettel fejezhető ki:
V = g * t
ahol:
V = sebesség, m/mp
g = gravitációs gyorsulás (9,81 m/mp2),
t = az esési idő, mp.
Az esési idő alatt a test által megtett út (S), ebben az esetben az alábbi képlet szerint határozható meg:
S = 0,5 * g * t2
E képleteket használva és ismerve az esési időt, ki lehet számítani, hogy mekkora utat és milyen sebességgel tesz meg légüres térben a test tetszőleges idő alatt (az esés kezdetétől végéig). Azonban az ejtőernyős esése nem légüres térben, hanem a levegőben történik, ahol a sebesség növekedésének mértékében növekszik a légellenállás is, tehát mindezen jelenségek lényegesen bonyolultabbak lesznek.
A levegőben eső mindenféle testre két erő hat: a nehézségi erő, mely lefelé irányul, és a levegő ellenállási ereje, amely az előbbivel ellentétes irányú.
A szabadon eső ejtőernyős bizonyos ideig a nehézségi erő hatása alatt 9,81 m/mp gyorsulással halad, azonban a levegő ellenállása következtében sebessége (egyébként azonos feltételek között) sohasem éri el a légmentes térben bekövetkező esési sebességet. A sebesség növekedése mértékének megfelelően növekszik a levegő ellenállása, csökken a gyorsulás és a sebesség mindig lassabban nő, amíg be nem áll az a pillanat, amikor a levegő ellenállási ereje egyenlő nem lesz az eső test súlyával. Ezt az állapotot nevezzük egyensúlyi állapotnak. Az erők egyensúlya esetén semmiféle gyorsulás nincs, következésképpen nem változik meg a sebesség értéke sem. A test megtartja az egyensúly-bekövetkezés pillanatában meglevő sebességét. Azonban ez az eset csupán akkor áll fenn, ha a test állandó sűrűségű közegben esik. A valóságban az ejtőernyősnek a földhöz valóközeledése mértékében a levegő sűrűségének növekedése következtében az ellenállás növekszik, és a sebesség csökken. A tehetetlenség következtében a test sebessége kissé nagyobb lesz, mint az illető magasságban az erők egyensúlya esetén fennálló sebességnél.
Az eső test sebességét az erők egyensúlya esetében kritikus sebességnek szoktuk nevezni.
Az ejtőernyős kritikus szabadesési sebességét az alábbi képlettel határozhatjuk meg:
Vkr = ( P / ( C1 * p * l ) )0,5
Ahol P = az ejtőernyős súlya az ejtőernyővel együtt kg-ban – C1 ellenállástényező az ejtőernyős testméreteire vonatkoztatva (C1 középértéke 0,0975, az ejtőernyős függőleges esésekor C1 = 0,05), p (ro) = a levegő sűrűsége, l = az ejtőernyős testmagassága m-ben.
Kísérlettel megállapították, hogy a kritikus sebesség 1000 m magasságból végzett ugrásnál a 10., 11. másodpercben áll be. Ez alatt az idő alatt az ejtőernyős rendszerint 335-380 m-t süllyed. Nagy magasságokból végzett ugrásoknál, mely magasságokban a levegő sűrűsége kicsi, az esési sebesség nagyobb lesz, mint földközelben. A kritikus sebesség és annak beállási ideje szintén növekszik.
Az ejtőernyős esési sebességének megközelítő kiszámításához az 1000-2000 méter magasságig az alábbi képletek használhatók fel:
a) az esési sebesség: V = (g * t) – (0,46 * t2)
b) a megtett út: = (0,5 * g * t2) – (0,15 * t3)
ahol V = az esési sebesség a meghatározott másodperc végén,
g = a gravitációs gyorsulás:
0,46 és 0,15 = kísérletezéssel megválasztott tényezők,
S = az eséskor megtett út.
t = másodpercben kifejezett idő,
Ha az ejtőernyős vízszintesen haladó repülőgépből ugrik ki, a repülőgép elhagyása után az ejtőernyős a tehetetlenség alapján bizonyos ideig megtartja a vízszintes sebességet, amely azonban fokozatosan csökken. Ezért az ejtőernyős mozgási sebessége a függőleges (süllyedési sebesség) és a vízszintes sebességből tevődik össze. Ezen két sebesség eredője adja a geometriai összeget, amelyet összsebességnek nevezünk. Az összsebesség négyzete egyenlő a vízszintes és függőleges sebességek négyzeteinek összegével. A nehézségi erő és a tehetetlenségi erő hatására az ejtőernyős esési pályája görbe vonal, amelynek domború fele a repülőgép repülési irányának oldalán van.

Az esési sebesség növekedésével a vízszintes sebesség csökken (a levegő ellenállása miatt) és abban a pillanatban, amikor az ejtőernyős eléri a kritikus esési sebességet, a vízszintes sebesség nullával egyenlő.
A repülőgép sebessége abban a pillanatban, amikor az ejtőernyős kiugrik belőle, elég nagy és az ejtőernyős ellenállása szintén nagy. Éppen azért az ejtőernyős vízszintes sebessége gyorsan csökken, esési sebessége pedig fokozatosan növekszik.
Ennek következtében az eredő sebesség csökken. Az előzőekből kitűnik, hogy az ejtőernyős vízszintes sebessége attól függ, hogy a repülőgép az ugrás pillanatában milyen sebességgel halad. Minél nagyobb a sebesség, annál nagyobb a vízszintes sebesség és következésképpen annál nagyobb az ejtőernyős előrehaladása.
Abban az esetben, ha az ejtőernyős kezdő vízszintes sebessége nagy, akkor az időegységre eső magasságveszteség jelentéktelen, és annál kisebb, minél nagyobb a kezdősebesség.
Az ejtőernyős a kiugrás után bizonyos idő múlva – a kezdősebesség nagyságától és irányától függetlenül – eléri a kritikus sebességet.
Az összsebesség azon erők szempontjából fontos, amelyek az ejtőernyő kinyílás akkor keletkeznek. Az ejtőernyős teljes esési útjának összsebességét azonban nemcsak azért kell tudnunk, hogy az ejtőernyő terhelését meghatározhassuk. Ugyanis az ejtőernyős mozgási sebessége az esés valamelyik pillanatában minimális értékű. Ha az ejtőernyős ebben a pillanatban nyitja ki az ejtőernyőt, akkor a túlterhelés a repülőgép adott sebessége esetén a legkisebb, következésképpen az ejtőernyőst érő ütés is a legkisebb. Az esési sebesség gyors csökkenésének eredményeképpen az ejtőernyőst dinamikus ütés éri, aminek ereje mindenekelőtt az ejtőernyő nyitási pillanatában fennálló zuhanási sebességtől és az ejtőernyő kinyílási idejétől függ.
